数学は暗記教科！勉強方法を紹介します。

多くの学生は数学を苦手に感じているが、実は暗記教科であり、将来の役立つ教科でもある。

「数学はセンスがないとできない」
「勉強してもあまり意味がないのでは？」
と感じている学生さんや親御さんは、意外と多いのではないでしょうか。

実は数学は、コツさえつかめば習得できる“暗記教科”の一面があるうえ、将来にわたって役立つ重要な科目でもあります。学生時代に数学力を磨いておけば、同級生に差をつけられるだけでなく、社会に出てからの仕事にも大いに活かせるのです。

「数学＝苦手」というイメージを変えるための勉強法を詳しくご紹介します。
最後まで読み進めることで、数学に対する考え方がきっと変わるはず。
ぜひ最後までお付き合いください。

＼ 他教科のコツはこちら／

数学という教科とは

数学は暗記科目です。

よく勘違いされているのですが、センスがないと解けない問題は京大東大クラスの理系での入試問題で1問ほど出題される程度で、受験で対面する問題はしっかりと基礎ができていれば解けるようにできています。

では暗記科目というと、よく疑問として公式を覚えるのか？といったものが挙げられます。もちろん、公式を覚えるのにこしたことはありませんが、ここで伝えたいことは「正しく公式を扱えるか」、もっというと「問題の基本パターンの引き出しがいかにあるか」です。

有名な三平方の定理も公式そのものを覚えていても仕方がありません。
（例）直角三角形の2辺の長さがわかっており、もう1辺の長さを求めるにはどうするか→三平方の定理を使用する　この流れが分かっていなければ公式がわかっていても意味がありません。

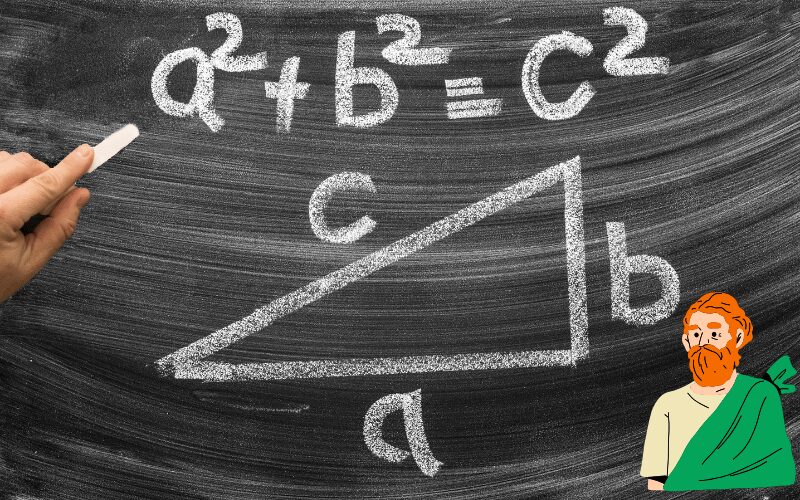
公式は計算を楽にする一種のツールであり、万能の道具ではありません。

例えば釘抜きを持っていたとしてもどこに釘があるのか、どのようにすれば釘が抜けるのかを知っていなければ使いこなせません。その道具の説明書もセットで覚える必要があります。
また複雑な作業をこなすのであれば道具の種類を増やす必要があります。

数学は教科書に載っているような基本的な問題パターンが組み合わさって受験問題のような応用問題へと仕上がります。このパターンを正しく記憶することで、複雑に組み合わさった問題を簡単な問へと分解することができます。

このパターンをいかに蓄えているかという意味で暗記教科と位置付けています。
英単語を見て、即座に日本語訳が出てくるように数学も基本的な問題を見て、すぐに解き方が頭に出てくるのが理想です。

反復方法（復習のコツ）

数学の問題は設計図を書くような作業です。

①.②.③ができれば数学の問題は90%は解けたようなものです。
どうしても計算のイメージがありますが、実際には「後は計算をすればよい」という所に持っていくまでが大変であり、問題の肝なのです。

復習する際は①〜③を脳内で再現できるようにしていきましょう。

数学は答えが決まっているのでその数値を覚えるのは簡単です。
ここまで述べた通り、答えの数値を覚えたところでそれは他の問題には応用できません。

どのような整理をして、なぜゴールをそこに設定したのか、なぜその公式を使う必要があるのか、他のアプローチの方が効率的ではないか、どのような要素が絡み合っているのか等を分析してください。そしてそのパターンや思考の手順を頭に染み込ませましょう。

私は数学の問題を復習する際には計算はあまり行いません。
④に至るまでの過程を反復していました。
そしてそのパターンを覚えると他の問題に応用できます。
これが正しい数学の復習法なのです。

まとめ

数学という教科は公式に焦点があてられて、それらを覚えて将来何の役に立つのかという質問をよく聞かれます。確かに各単元で出てくる公式を覚えていても、それがそのまま生活の役に立つ場面は少ないでしょう。

しかし、数学的な思考＝問題を整理し、仮説検証を行っていくことが重要なのです。

親御さんの方が理解しやすいと思います。
社会に出た際には答えのない問について考えることが日常的になります。

これらについて一定の答えを出していく際に、状況や何が問題なのかをまず整理して、その解決法を考えていきます。その解決法が正しいか検証し、次の行動をブラッシュアップしていきます。
これはまさに数学で鍛えられる部分です。

数学は、目の前の問題を解くだけでなく、未来を切り開く力を育てる教科です。
仮説を立て、検証し、結論を導く力は、どの分野でも必ず役立ちます。
『考える力』を鍛えられると信じて、ぜひ挑戦を続けてください

＼ 無料で学習ポイント発信／